A Review of the Blockchain/Bitcoin white paper
Disclaimer:
In this post, I will review the Blockchain white paper - Bitcoin: A Peer-to-Peer Electronic Cash System. The paper is regarded as the first system utilising Blockchain technology. My goal is to understand Blockchain as a technology forward, and it has nothing to do with investing in Bitcoins. For the later, Reddit may be a great place
Some words before I start:
After reading the paper, unsurprisingly, the extent of the topic may be beyond my comprehension. I, therefore, will try to address the concepts of Hash, Distributed Computing, maybe B-money before moving into Blockchain. From the paper, it seems to be Bitcoin was purely an incentive scheme, and Blockchain was the main concept of the paper. Hence, I am a little puzzled why the title was “Bitcoin (Rather than Blockchain): A Peer-to-Peer Electronic Cash System”. anyway, let’s dive in.
Hash Function:
A hash function is any function that can be used to map data of arbitrary size to fixed-size values. The values returned by a hash function are called hash values, hash codes, digests, or simply hashes. The values are usually used to index a fixed-size table called a hash table. The use of a hash function to index a hash table is called hashing or scatter storage addressing.
The paper proposed the usage of SHA-256 as a way to allow extensive computational work (therefore acting as a proof of work). SHA-256 falls into the family of SHA-2. SHA-2 (Secure Hash Algorithm 2) is a set of cryptographic hash functions designed by the United States National Security Agency (NSA) and first published in 2001. They are built using the Merkle–Damgård construction, from a one-way compression function itself built using the Davies–Meyer structure from a specialized block cypher.
SHA-256 is a novel hash function computed with 32-bit words. Here I need to explain what a one-way compression system is and how Merkle–Damgård construction and Davies-Meyer structure play the part.
One-way compression system, Merkle–Damgård construction and Davies-Meyer structure:
In cryptography, a one-way compression function is a function that transforms two fixed-length inputs into a fixed-length output. The transformation is “one-way”, meaning that it is difficult given a particular output to compute inputs that compress to that output. One-way compression functions are not related to conventional data compression algorithms, which instead can be inverted exactly (lossless compression) or approximately (lossy compression) to the original data.
A one-way function is a function that is easy to compute but hard to invert. A one-way compression function (also called hash function) should have the following properties:
- Easy to compute: If you have some input(s), it is easy to calculate the output.
- Preimage-resistance: If an attacker only knows the output it should be infeasible to calculate an input. In other words, given an output h, it should be unfeasible to calculate an input m such that hash(m)=h;
- Second preimage-resistance: Given an input m1 whose output is h, it should be infeasible to find another input m2 that has the same output h i.e. hash(m1) does not equal to hash(m2).
- Collision-resistance: It should be hard to find any two different inputs that compress to the same output i.e. an attacker should not be able to find a pair of messages m1 does not equal to m2. such that hash(m1) does not equal hash(m2). Due to the birthday paradox (see also birthday attack) there is a 50% chance a collision can be found in time of about 2^(n/2) where n is the number of bits in the hash function’s output. An attack on the hash function thus should not be able to find a collision with less than about 2^(n/2) work.
I think Merkle–Damgård construction and Davies-Meyer structure deserved separates posts, and to simplify things (with helps from Wikipedia ), a few brief words on these two topics:
Merkle–Damgård construction consists of three parts: starting from initial values, also called initialisation vector (IV), it is a fixed value (algorithm or implementation specific). The next block is the compression (or compacting) function f that takes the result so far, combines it with the message block, and produces an intermediate result. There can be a chain of these f function. The last part is a finalisation block that pads the results from a chain of with zeros. his is crucial to the security of this construction
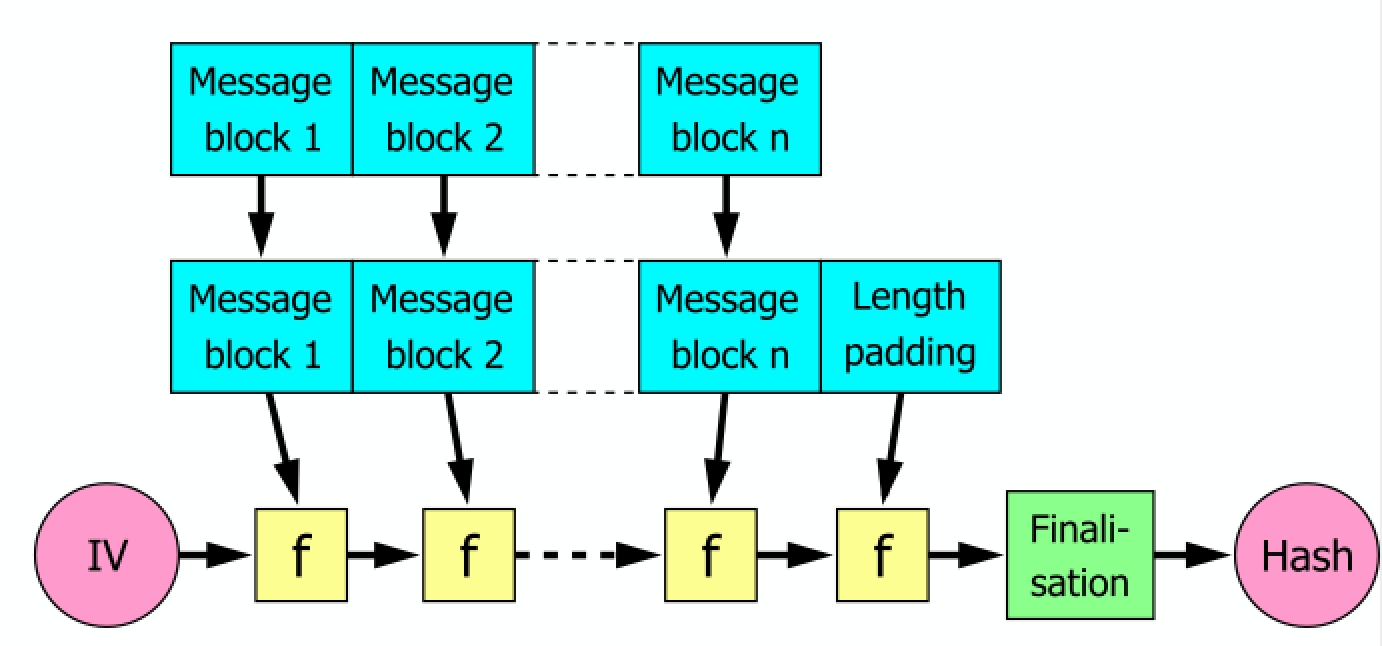
The above figure is from Wikipedia) by Davidgothberg. A hash function must be able to process an arbitrary-length message into a fixed-length output. This can be achieved by breaking the input up into a series of equal-sized blocks, and operating on them in sequence using a one-way compression function.
Davies-Meyer structure is a compression function (the yellow block in the image above, i.e. the function f) feeds each block of the message as a key to block cypher. It takes the previous Hash value \( H_{i-1} \) as the plaintext to be encrypted. The output ciphertext is then also XORed (⊕) (For XO Gate, see my previous post ) with the previous hash value \(H_{i−1} \)to produce the next hash value \( H_{i} \). In the first round when there is no previous hash value it uses a constant pre-specified initial value (\(H_{0}\) i.e. IV).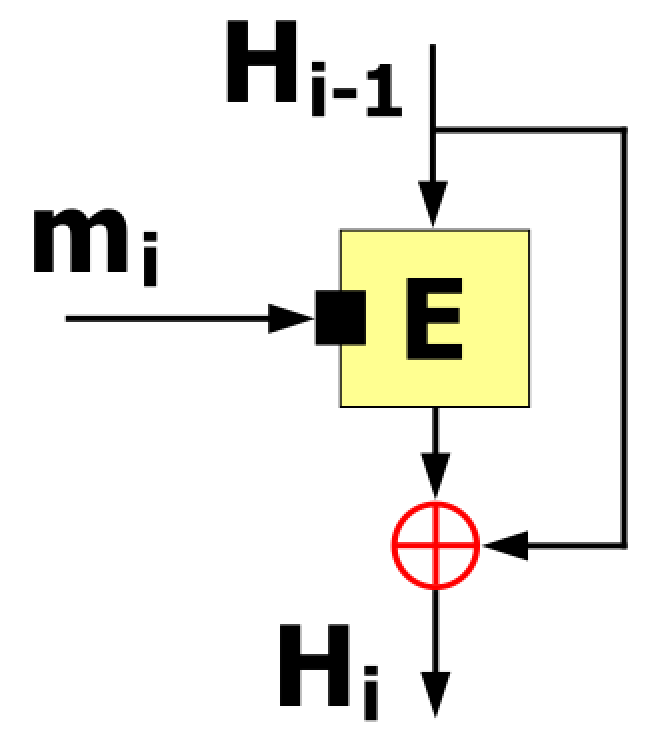
The above figure is from Wikipedia) by Davidgothberg.
Summary of Blockchain System:
Finally, Let’s talk about blockchain.
Here are the main take-away points (direct quotes):
- The key motivation for Blockchain is to “What is needed is an electronic payment system based on cryptographic proof instead of trust, allowing any two willing parties to transact directly with each other without the need for a trusted third party.”
- Transactions that are computationally impractical to reverse would protect sellers from fraud, and routine escrow mechanisms could easily be implemented to protect buyers
- The paper purposes a solution to the double-spending problem using a peer-to-peer network.
- The system is secure as long as honest nodes collectively control more CPU power than any cooperating group of attacker nodes
With those in mind, we shall dive in the technical aspects of the technology. The so called blockchain contains a network of “Hash block” (AKA, Block, Node..etc..). Each hash contains a block of items to be timestamped and widely published. When the block becomes timestamped, it contains the previoud Hash, Nonce and all the transactions it collects.
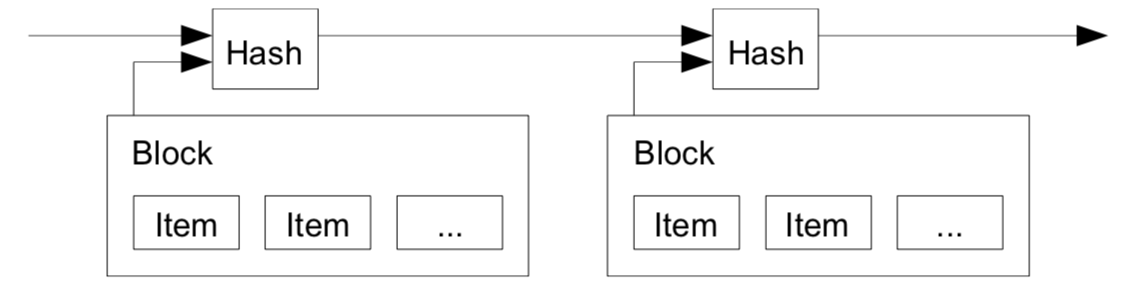
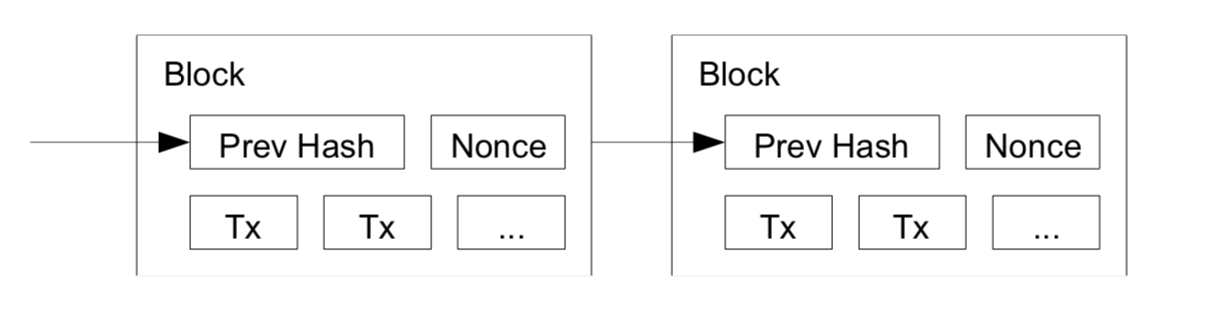
To answer the question of what timestamp or Nonence is, we have to go back to the motivation of Blockchain, which is really a decentralised payment system. Therefore, Timestamp (or timestamp Server as purposed in the paper ) is a solution to prevent double-spent. A direct quote from the paper:
” The only way to confirm the absence of a transaction is to be aware of all transactions. In the mint based model, the mint was aware of all transactions and decided which arrived first. To accomplish this without a trusted party, transactions must be publicly announced, and we need a system for participants to agree on a single history of the order in which they were received.”
In the above sentence, there is the “mint model”, which is the trusted central authority that checks every transaction for double-spending. For example a bank, however, we would like a decentralised payment system, therefore to remove the bank/trusted party, we use blockchain that has information of all previous transactions
Therefore if a block is timestamped, it means the data must have existed at the time. Each timestamp includes the previous timestamp in its hash, forming a chain, with each additional timestamp reinforcing the ones before it.
Here comes the most important concept–Proof-of-Work: This step is essential to implement a distributed timestamp server on a peer-to-peer basis and form the first defence from the attacker. The proof-of-work involves solving a maths question which can be SHA-256. As a cryptographic method, it is pretty hard to decrypt it, if not impossible at all. The details, we scan for a value that when hashed (for example, using SHA-256), the hash begins with a number of zero bits. We also implement a nonce in the block until a value is found that gives the block’s hash the required zero bits (for more details see Adam Back’s Hashcash, link in the reference). This is a pretty energy-intense process and requires a lot of CPU effort. This proof-of-work is commonly known as “Mining”. Once the CPU has been expanded to make it satisfy the proof-of-work, the block cannot be changed without redoing this work. As later blocks are chained after it, the work to change the block would include redoing all the blocks after it. A side note is the average work required is exponential in the number of zero bits required and can be verified by executing a single hash.
Let’s now look at how to run the whole network: Here are the steps summarized in the paper:
- New transactions are broadcast to all nodes.
- Each node collects new transactions into a block.
- Each node works on finding a difficult proof-of-work for its block.
- When a node finds a proof-of-work, it broadcasts the block to all nodes.
- Nodes accept the block only if all transactions in it are valid and not already spent.
- Nodes express their acceptance of the block by working on creating the next block in the chain, using the hash of the accepted block as the previous hash.
Here comes another important concept–“Nodes always consider the longest chain to be the correct one and will keep working on extending it”. Two additional scenarios to be considered:
- If two nodes broadcast different versions of the next block simultaneously, they can work on the first one they received and save the other in case it becomes longer. The tie will be broken when the next proof-of-work is found and one branch becomes longer; the nodes that were working on the other branch will then switch to the longer one.
- If a node does not receive a block, it will request it when it receives the next block and realizes it missed one.
Secruity and Privacy :
To summarise, there are three ways to ensure the security of the chain:
- The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it. If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains.
- The incentive (AKA Bitcoin) for packing all transaction into a block gives the attacker reason to use his CPU power to build extend the chain, instead of defrauding people by stealing back his payments.
- If the network is overpowered by an attacker, we can accept alerts from network nodes when they detect an invalid block, prompting the user’s software to download the full block and alerted transactions to confirm the inconsistency.
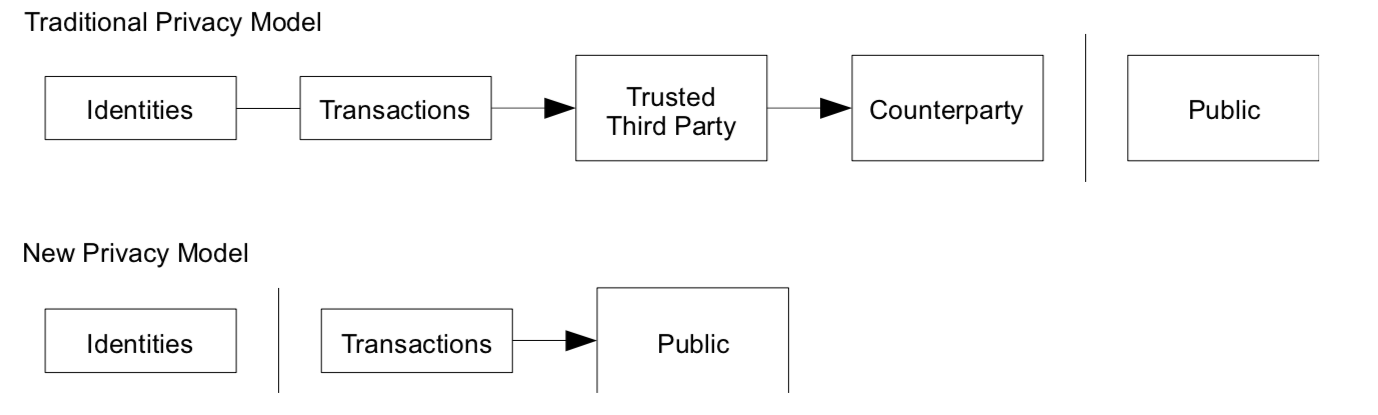
The paper also purposes a different way to protect payees identify. As opposed to a traditional bank, Blockchain requires all transactions to be public. Privacy is achieved with anonymous public keys. The public can see that someone is sending an amount to someone else but have no information about the sender nor receiver. An additional firewall should be issued by using a new key pair for each transaction. It reduces the risk of a corrupted key exposing all transaction of the same owner.
Bitcoin:
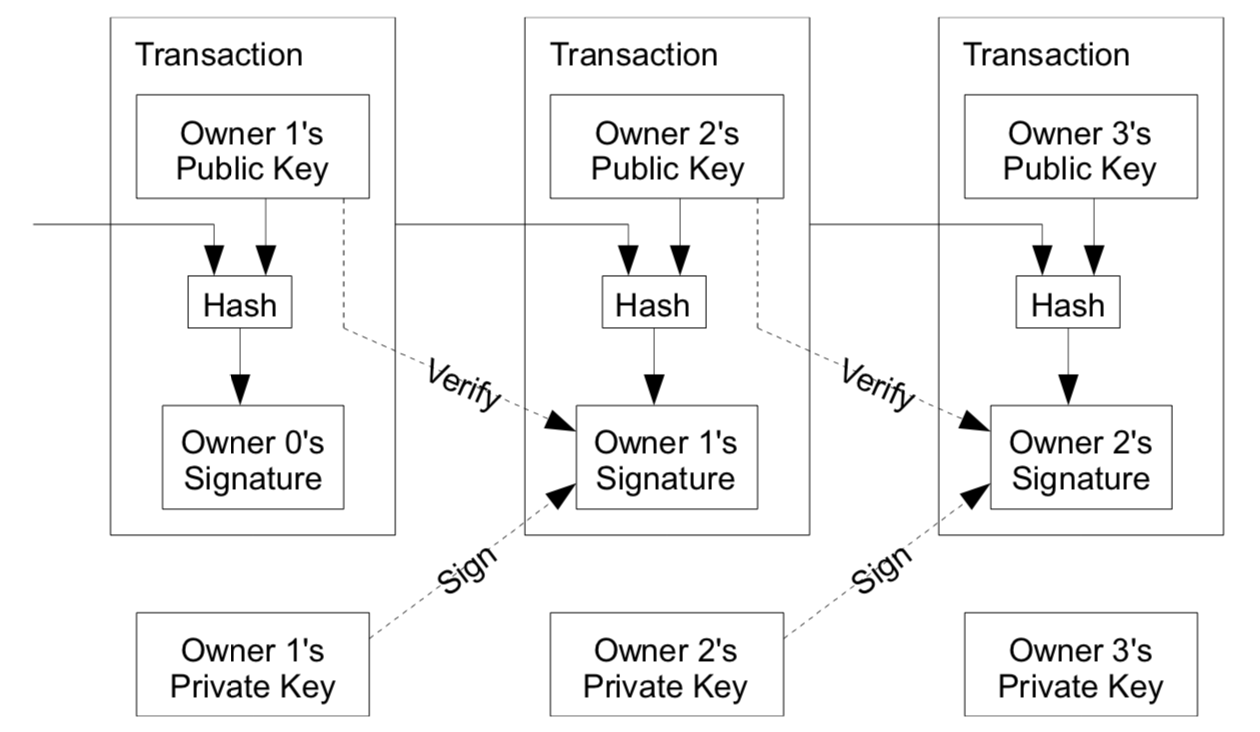
To understand the role of Bitcoin, we have to go back to the motivation of Blockchain–A decentralised Payment system !! Hereby the paper defined an electronic coin (AKA bitcoin) as a chain of a digital signature. It works in the follwoing way :
- Each owner transfers the coin to the next by digitally signing a hash of the previous transaction and the public key of the next owner and adding these to the end of the coin.
- A payee can verify the signatures to verify the chain of ownership.
- The problem of the payee can’t verify that one of the owners did not double-spend the coin is solved by being aware of all transactions.
Other than being a ledger, bitcoin has an essential incentive role that keeps people working to extend the longest chain. “By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. “. This incentive has two impacts:
- Encourage nodes to support the network
- Act as a central authority to initially issue and distribute coins into circulation.
“The steady addition of a constant amount of new coins is analogous to gold miners expending resources to add gold to circulation. In our case, it is CPU time and electricity that is expended.”
Since only a predetermined number of coins is allowed to circulate the system, the system can be complete inflation-free while incentive comes from charging a transaction fee.
Final Remarks:
There are a few things in the paper I decided not to include here, but if you are interested, please check them out: 1. Reclaiming Disk Space, 2. Simplified Payment Verification 3. Combining and Splitting Value. 4. Calculations.
The paper omitted a few technical aspects of Blockchain, for example
- why there is a predetermined number of bitcoin in the system
- why the value of bitcoin diminish with time,
- how public and private keys work and how they are distributed
- What mathematical methods are required to do the proof-of-work and why it requires so much CPU power
- etc…
To answer these questions, you need to review a few cryptography books as well as some work by the true Pioneers of Blockchain –W.Dai, A. Back, R.C. Merkle, D.Bayer and many more. Some useful resources are in the references if you are interested.
Referenece:
- SECRECY, AUTHENTICATION, AND PUBLIC KEY SYSTEMS, Ralph Charles Merkle, 1979
- Bitcoin: A Peer-to-Peer Electronic Cash System
- W. Dai, “b-money,” 1998.
- H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal trust requirements,” In 20th Symposium on Information Theory in the Benelux, May 1999.
- S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In Journal of Cryptology, vol 3, no2, pages 99-111, 1991.
- D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,” In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
- S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.
- A. Back, “Hashcash - a denial of service counter-measure,” 2002
- R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
- W. Feller, “An introduction to probability theory and its applications,” 1957.
