Second Order Total Variation Diminishing scheme: MUSCL-Hancock with Superbee slope limiter -Ghost Fluid Method Serie 2
This article depicts a high resolution methods that also ensureS TVD nature of the scheme
HLLC solver through provides a good approximation for intermediate states but is first order accurate. In this study, I used a second order scheme to simulate with the highest possible resolution. The scheme is known as MUSCL-Hancock, which aims to construct a flux that is second order extension of the first order upwind scheme. The scheme involves three steps: Data Reconstruction, Evolution and Solving a Riemann Problem. The first step involves linear extrapolation of cell centered states to obtains cell boundary values
\[U^L_i = U^n_i - \frac{1}{2} \Delta i\] \[U^R_i = U^n_i - \frac{1}{2} \Delta i\] where $ \Delta i$ is \[\Delta i = \frac{1}{2}(1+w)\Delta_{i+\frac{1}{2}} + \frac{1}{2}(1-w)\Delta_{i+\frac{1}{2}}\] \[\Delta_{i-\frac{1}{2}} = U^n_i -U^n_i+1\] \[\Delta_{i+\frac{1}{2}} = U^n_{i+1} -U^n_i\]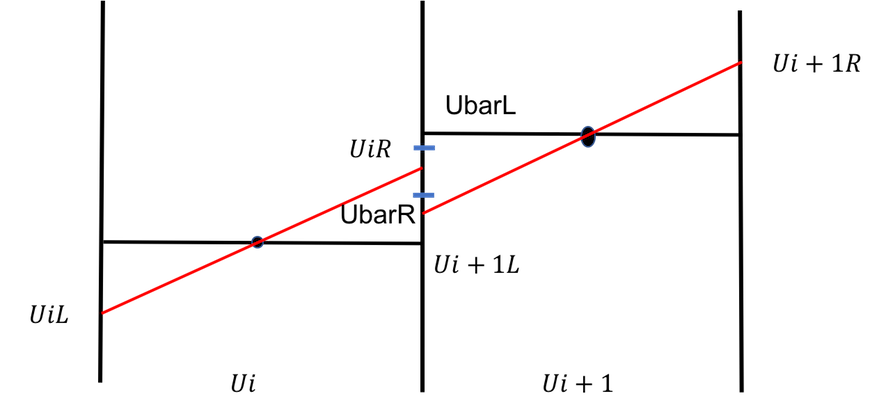
The second step involves finding the intermediate states using the extrapolated values for half a time step:
\[\bar{U^L_i} = U^L_i + \frac{1}{2}\frac{\Delta t}{ \Delta x}(F(U^L_i) - F(U^R_i))\] \[\bar{U^R_i} = U^R_i + \frac{1}{2}\frac{\Delta t}{ \Delta x}(F(U^L_i) - F(U^R_i))\] The fluxes obtained from the extrapolated state vectors are boundary fluxes which is not equivalent to inter cell fluxes. The final stage involves solving a Riemann problem between $ \bar{U^L_i}$ and $\bar{U^R_i}$. In this study, HLLC solver is used. Other solver such as First Order Centered Scheme (FORCE) also exists. To make our solution total variation diminishing, I incorporate the super-bee slope limiter upon calculating $\Delta i$. The new limited slope is calculated via : \[\bar{\Delta_i} = \xi \Delta_i\] where $\xi (r)$ is known as the slope limiter and can be found from: \[\begin{cases} r = \frac{\Delta_{i-\frac{1}{2}}}{\Delta _{i+\frac{1}{2}}}\\ \xi_R(r) = \frac{ 2 \beta _{i - \frac{1}{2}}r}{1-w + (1+w)r} & \quad \beta_{i-\frac{1}{2}} = \frac{2}{1+c} \\ \end{cases}\] \[\xi_{sb}(r) = \begin{cases} 0, & \quad \quad \quad \text{if } r \leq 0 \\ 2r, & \quad \quad \quad \text{if } 0 \leq r \leq \frac{1}{2}\\ 1, & \quad \quad \quad \text{if } \frac{1}{2} \leq r \leq 1\\ min{r, \xi_R(r),2}, & \quad \quad \quad \text{if} r \geq2 \end{cases}\] c is the Courant number for the single wave present, and $w$ and $\beta$ are taking values of 0 and 1 respectively. Other slope limiter like van Leer or Minbee-type are also available. Superbee is used in this study as it is the least diffusive one, helping to maintain the sharpness of discontinuities \cite{VanLeer1984} , \cite{Quirk1994}.References
- Toro, E. F. (2009), Riemann Solvers and Numerical Methods for Fluid Dynamics, thrid ed., Springer.
- Van Leer, B. (1976), MUSCL, a new approach to numerical gas dynamics., Computing in plasma physics and astrophysics, (January 1976).
- Toro, E. F., M. Spruce, and W. Speares (1994), Restoration of the contact surface in the HLL-Riemann solver, Shock Waves, 4 (1), 25–34, doi:10.1007/BF01414629.
- Van Leer, B. (1977a), Towards the ultimate conservative difference scheme. IV. A new ap- proach to numerical convection, Journal of Computational Physics, 23(3), 276–299, doi: 10.1016/0021-9991(77)90095-X.
- Van Leer, B. (1977b), Towards the Ultimate Conservative Difference Scheme III. Upstream- Centered Finite-Difference Schemes for Ideal Compressible Flow, Journal of Computational Physics, 275(23), 263–275.
- Van Leer, B. (1979), Towards the Ultimate Conservative Difference Scheme V. A Second- Order Sequel to Godnov, Journal of Computational Physics, 32(1), 101–136, doi:10.1016/0021- 9991(79)90145-1.
- Van Leer, B. (1984), On the Relation Between the Upwind-Differencing Schemes of Godunov, EngquistOsher and Roe Share on, SIAM Journal on Scientific and Statistical Computing, 5(1), doi:10.1137/0905001.
